LE DIVINE PROPORZIONI
Fermo, Palazzo dei Priori, 30 luglio – 4 novembre 2004

Nella Mostra di Fermo i modelli sono stati inseriti in un suggestivo percorso, progettato dall’arch. Giuliano Gresleri, che ha ricostruito il cammino di ricerca ed elaborazione condotta dai due autori, a partire dalla forte suggestione iniziale esercitata su di loro dal dipinto di Jacopo de Barbari in cui il frate matematico Luca Pacioli viene ritratto nel suo studio, mentre illustra gli Elementi di Euclide ad un illustre allievo, Guidubaldo da Montefeltro; nel dipinto figurano due solidi geometrici: un dodecaedro, appoggiato su di un libro ed un solido trasparente sospeso ad un filo.
Dal ritratto di Luca Pacioli e dalla sua opera De Divina Proportione Romano e Francesca Folicaldi hanno preso le mosse per un lavoro che rappresenta, a nostro avviso, uno straordinario esempio di laboratorio di storia della scienza , nel quale la ricerca storica condotta sui testi originali si accompagna con la sperimentazione pratica delle tecniche e dei prodotti descritti nei documenti.
E’ in questo modo che la realizzazione dei modelli è avanzata di pari passo con la rilettura del Libro VII della Repubblica e del Timeo, alla scoperta di un Platone matematico, che pone la matematica e la geometria dei solidi tra le discipline necessarie alla formazione filosofica dei giovani.
E’ nel Timeo che Platone affronta il tema della creazione del cosmo, introducendo i cinque solidi regolari come elementi di cui il Demiurgo si serve per conferire forma, proporzione e visibilità al mondo sensibile.
“ E prima di tutto questo, tutte le cose si trovavano senza ragione [ ragione = proporzione; ] e senza misura. Ma quando Dio intraprese ad ordinare l’universo, il fuoco in primo luogo e l’aria e l’acqua e la terra, avevano bensì qualche traccia di sé, ma si trovavano in quella condizione in cui è naturale si trovi ogni cosa, quando il Dio è assente. Queste cose, dunque, che si trovavano in questo stato Egli in primo luogo le modellò con forme e numeri” ( 53B ).
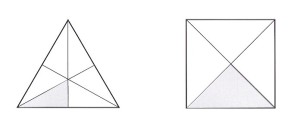
Due triangoli rettangoli sono alla base della formazione delle superfici che delimitano i corpi solidi dei quattro elementi: il primo ( “il più bello” ) ha un cateto doppio dell’altro; il secondo è isoscele.
Dall’unione di sei triangoli del primo tipo nasce il triangolo equilatero; dall’unione di quattro triangoli del secondo tipo nasce il quadrato.
La piramide o tetraedro è il primo solido regolare che si forma con l’unione di 4 triangoli equilateri, ognuno composto da 6 triangoli scaleni. E’ il solido che viene associato all’elemento fuoco.
Il secondo solido, l’ottaedro, costituito da 8 triangoli equilateri ( 8×6 = 48 triangoli scaleni ) è associato all’aria; l’icosaedro, composto da 20 triangoli equilateri ( 20×6=120 triangoli scaleni ) è associato all’acqua; il cubo o esaedro, composto da 6 quadrati ( 6×4= 24 triangoli rettangoli isosceli ) è associato alla terra. Essendo possibile, infine, costruire solo un quinto solido regolare, il dodecaedro ( composto da 12 facce pentagonali ), Dio se ne servi come immagine dell’universo nella sua totalità ( per “decorare l’universo”). Al cosmo, invece, è attribuita la forma sferica, la più perfetta, che comprende in sé tutte le altre forme.
Tutte queste forme sono da intendersi di dimensioni così piccole da risultare invisibili singolarmente; solo quando esse si aggregano in numero sufficientemente grande le masse diventano visibili
La divina proporzione
E’ interessante notare come Platone attribuisca alla proporzione un ruolo fondamentale nel tenere uniti gli elementi che danno visibilità al mondo.
“ Ma che due cose si compongano bene da sole, prescindendo da una terza, in maniera bella, non è possibile. Infatti vi deve essere in mezzo un legame che congiunga l’una con l’altra. … E questo per sua natura nel modo più bello compie la proporzione. Infatti, allorché di tre numeri, o masse, o potenze quali si vogliano, il medio sta all’ultimo come il primo sta al medio, e ulteriormente, a sua volta, quello medio sta al primo come l’ultimo sta a quello medio, allora il medio diventando primo ed ultimo, e l’ultimo e il primo diventando ambedue medi, in questa maniera, di necessità accadrà che tutte le proporzioni siano le stesse, e, divenute fra di loro le stesse, tutte saranno un’unità”(31C-32A).
La proporzione di cui parla Platone è la proporzione geometrica, l’uguaglianza tra due rapporti del tipo a : b = c : d ( ‘rapporto’ è logos, in greco e ratio ‘ragione’ in latino; ana-logos, ‘proporzione’). In particolare Platone si riferisce a quella particolare proporzione nella quale i termini medi sono uguali tra loro; il termine medio, funge quindi da collegamento tra i due estremi.
Una delle applicazioni più interessanti di questo tipo di proporzione è la divisione di un segmento in media ed estrema ragione ( secondo la definizione data da Euclide nel VI Libro degli Elementi ); è la proporzione che Luca Pacioli definì divina e Leonardo sezione aurea in ragione della “gradevolezza” e dell’armonia che sembrano caratterizzare le forme costruite secondo quella proporzione.
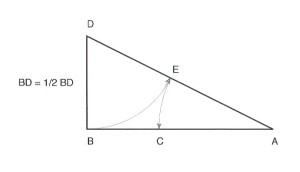
A partire dal segmento AB si costruisca su di esso il triangolo rettangolo “platonico” , alzando da B il cateto BD di lunghezza uguale ad AB/2. Con il compasso puntato in D si riporti BD su AD, individuando il punto E. Puntando il compasso in A co apertura AE si intersechi AB in C.
Il segmento AC determinato in tal modo è il medio proporzionale tra il segmento DC < AC e l’intero segmento AB.
L’apparente semplicità di questa costruzione con riga e compasso nasconde un aspetto che risultò traumatico per i pitagorici del V sec. a.C., che avevano visto il numero come entità perfetta capace di ordinare il mondo e il pensiero. Si tratta del problema della incommensurabilità di questo rapporto, non riconducibile a un numero intero o frazionario, un numero razionale.
Il Numero d’oro, indicato con Φ in omaggio dello scultore greco Fidia, nelle cui opere è possibile ritrovare questa proporzione, è un numero irrazionale, che protrae disordinatamente le sue cifre decimali all’infinito : Φ = 1,6180339887…
Il numero comparirà ancora nel pensiero matematico di Leonardo Pisano, detto Fibonacci, nell’opera di Luca Pacioli e in quella di Keplero e nei campi apparentemente più distanti, dall’arte e dalla teoria del bello, alla botanica, alla biologia, nella musica dell’età barocca e dell’età contemporanea.